(
QED), a relativistic quantum field theory of electrodynamics, is among the most stringently tested theories in
physics.
The most precise and specific tests of QED consist of measurements of the electromagnetic
fine structure constant, α, in various physical systems. Checking the consistency of such measurements tests the theory.
Tests of a theory are normally carried out by comparing experimental results to theoretical predictions. In QED, there is some subtlety in this comparison, because theoretical predictions require as input an extremely precise value of α, which can only be obtained from another precision QED experiment. Because of this, the comparisons between theory and experiment are usually quoted as independent determinations of α. QED is then confirmed to the extent that these measurements of α from different physical sources agree with each other.
The agreement found this way is to within ten parts in a billion (10
−8), based on the comparison of the
electron anomalous magnetic dipole moment and the
Rydberg constant from atom recoil measurements as described below. This makes QED one of the most accurate physical theories constructed thus far.
Besides these independent measurements of the fine-structure constant, many other predictions of QED have been tested as well.
Measurements of the fine-structure constant using different systems [edit]
Precision tests of QED have been performed in low-energy
atomic physics experiments, high-energy
collider experiments, and
condensed matter systems. The value of α is obtained in each of these experiments by fitting an experimental measurement to a theoretical expression (including higher-order
radiative corrections) that includes α as a parameter. The uncertainty in the extracted value of α includes both experimental and theoretical uncertainties. This program thus requires both high-precision measurements and high-precision theoretical calculations. Unless noted otherwise, all results below are taken from.
[1]
Low-energy measurements [edit]
Anomalous magnetic dipole moments [edit]
- 1) A precise measurement of the anomalous magnetic dipole moment, and
- 2) A precise theoretical calculation of the anomalous magnetic dipole moment in terms of α.
As of February 2007, the best measurement of the anomalous magnetic dipole moment of the electron was made by Gabrielse et al.
[3] using a single electron caught in a
Penning trap. The difference between the electron's cyclotron frequency and its spin precession frequency in a magnetic field is proportional to g−2. An extremely high precision measurement of the quantized energies of the cyclotron orbits, or
Landau levels, of the electron, compared to the quantized energies of the electron's two possible
spin orientations, gives a value for the electron's spin
g-factor:
- g/2 = 1.001 159 652 180 85 (76),
a precision of better than one part in a trillion. (The digits in parentheses indicate the uncertainty in the last listed digits of the measurement.)
The current state-of-the-art theoretical calculation of the anomalous magnetic dipole moment of the electron includes QED diagrams with up to four loops. Combining this with the experimental measurement of g yields the most precise value of α:
[4]- α−1 = 137.035 999 070 (98),
a precision of better than a part in a billion. This uncertainty is ten times smaller than the nearest rival method involving atom-recoil measurements.
A value of α can also be extracted from the anomalous magnetic dipole moment of the
muon. The g-factor of the muon is extracted using the same physical principle as for the electron above – namely, that the difference between the cyclotron frequency and the spin precession frequency in a magnetic field is proportional to g−2. The most precise measurement comes from
Brookhaven National Laboratory's muon g−2 experiment,
[5] in which polarized muons are stored in a cyclotron and their spin orientation is measured by the direction of their decay electrons. As of February 2007, the current world average muon g-factor measurement is,
[6]- g/2 = 1.001 165 920 8 (6),
a precision of better than one part in a billion. The difference between the g-factors of the muon and the electron is due to their difference in mass. Because of the muon's larger mass, contributions to the theoretical calculation of its anomalous magnetic dipole moment from
Standard Model weak interactions and from contributions involving
hadrons are important at the current level of precision, whereas these effects are not important for the electron. The muon's anomalous magnetic dipole moment is also sensitive to contributions from new physics
beyond the Standard Model, such as
supersymmetry. For this reason, the muon's anomalous magnetic moment is normally used as a probe for new physics beyond the Standard Model rather than as a test of QED.
[7]
Atom-recoil measurements [edit]
This is an indirect method of measuring α, based on measurements of the masses of the electron, certain atoms, and the
Rydberg constant. The Rydberg constant is known to seven parts in a trillion. The mass of the electron relative to that of
caesium and
rubidium atoms is also known with extremely high precision. If the mass of the electron can be gotten with high enough precision, then α can be found from the Rydberg constant according to

To get the mass of the electron, this method actually measures the mass of an
87Rb atom by measuring the recoil speed of the atom after it emits a photon of known wavelength in an atomic transition. Combining this with the ratio of electron to
87Rb atom, the result for α is,
[8]- α−1 = 137.035 998 78 (91).
Because this measurement is the next-most-precise after the measurement of α from the electron's anomalous magnetic dipole moment described above, their comparison provides the most stringent test of QED, which is passed with flying colors: the value of α obtained here is within one standard deviation of that found from the electron's anomalous magnetic dipole moment, an agreement to within ten parts in a billion.
Neutron Compton wavelength [edit]
This method of measuring α is very similar in principle to the atom-recoil method. In this case, the accurately known mass ratio of the electron to the
neutron is used. The neutron mass is measured with high precision through a very precise measurement of its
Compton wavelength. This is then combined with the value of the Rydberg constant to extract α. The result is,
- α−1 = 137.036 010 1 (5 4).
Hyperfine splitting [edit]
Hyperfine splitting is a splitting in the energy levels of an
atom caused by the interaction between the
magnetic moment of the
nucleus and the combined
spin and orbital magnetic moment of the electron. The hyperfine splitting in
hydrogen, measured using
Ramsey's hydrogen
maser, is the most precisely known quantity in physics. Unfortunately, the influence of the
proton's internal structure limits how precisely the splitting can be predicted theoretically. This leads to the extracted value of α being dominated by theoretical uncertainty:
- α−1 = 137.036 0 (3).
The hyperfine splitting in
muonium, an "atom" consisting of an electron and an antimuon, provides a more precise measurement of α because the muon has no internal structure:
- α−1 = 137.035 994 (18).
Lamb shift [edit]
The
Lamb shift is a small difference in the energies of the 2 S
1/2 and 2 P
1/2 energy levels of hydrogen, which arises from a one-loop effect in quantum electrodynamics. The Lamb shift is proportional to α
5 and its measurement yields the extracted value:
- α−1 = 137.036 8 (7).
Positronium [edit]
Positronium is an "atom" consisting of an electron and a
positron. Whereas the calculation of the energy levels of ordinary hydrogen is contaminated by theoretical uncertainties from the proton's internal structure, the particles that make up positronium have no internal structure so precise theoretical calculations can be performed. The measurement of the splitting between the 2
3S
1 and the 1
3S
1 energy levels of positronium yields
- α−1 = 137.034 (16).
Measurements of α can also be extracted from the positronium decay rate. Positronium decays through the annihilation of the electron and the positron into two or more
gamma-ray photons. The decay rate of the singlet ("para-positronium")
1S
0 state yields
- α−1 = 137.00 (6),
and the decay rate of the triplet ("ortho-positronium") 3S1 state yields
- α−1 = 136.971 (6).
This last result is the only serious discrepancy among the numbers given here, but there is some evidence that uncalculated higher-order quantum corrections give a large correction to the value quoted here.
High-energy QED processes [edit]
The
cross sections of higher-order QED reactions at high-energy electron-positron colliders provide a determination of α. In order to compare the extracted value of α with the low-energy results, higher-order QED effects including the running of α due to
vacuum polarization must be taken into account. These experiments typically achieve only percent-level accuracy, but their results are consistent with the precise measurements available at lower energies.
The cross section for

yields
- α−1 = 136.5 (2.7),
and the cross section for

yields
- α−1 = 139.9 (1.2).
Condensed matter systems
The quantum Hall effect yields
- α−1 = 137.035 997 9 (3 2),
and the AC Josephson effect yields
- α−1 = 137.035 977 0 (7 7).
Other tests [edit]
- QED predicts that the photon is a massless particle. A variety of highly sensitive tests have proven that the photon mass is either zero, or else extraordinarily small. One type of these tests, for example, work by checking Coulomb's law at high accuracy, as Coulomb's law would be modified if the photon mass were nonzero. See the article Photon#Experimental checks on photon mass.
- QED predicts that when electrons get very close to each other, they behave as if they had a higher electric charge, due to vacuum polarization. This prediction was experimentally verified in 1997 using the TRISTAN particle accelerator in Japan.[9]
 ,
,![\mathcal{L} = \frac{1}{2}\left(\mathbf{E}^{2}-\mathbf{B}^{2}\right)+\frac{2\alpha^{2}}{45 m^{4}}\left[\left(\mathbf{E}^2 - \mathbf{B}^2\right)^{2} + 7 \left(\mathbf{E}\cdot\mathbf{B}\right)^{2}\right]](http://upload.wikimedia.org/math/2/d/9/2d9565d4a7c928e42aa482181e2c26f7.png)
![\mathcal{L} =-\mathcal{F} -\frac{1}{8\pi^{2}}\int_{0}^{\infty}\frac{ds}{s^{3}}\exp\left(-m^{2}s\right)\left[(es)^{2}\frac{\operatorname{Re}\cosh\left(es\sqrt{2\left(\mathcal{F} + i\mathcal{G}\right)}\right)}{\operatorname{Im}\cosh\left(es\sqrt{2\left(\mathcal{F} + i\mathcal{G}\right)}\right)}\mathcal{G}-\frac{2}{3}(es)^{2}\mathcal{F} - 1\right]](http://upload.wikimedia.org/math/c/b/c/cbc318ac85e0a9350ff0d7df33427d68.png)


 yields
yields yields
yields

 is the
is the  is the scattering angle.
is the scattering angle.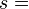










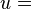


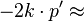



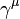 are the
are the  are the four-component spinors for fermions, while
are the four-component spinors for fermions, while are the four-component spinors for anti-fermions (see
are the four-component spinors for anti-fermions (see 





 :
:




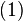

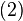






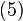
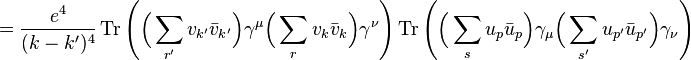
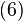
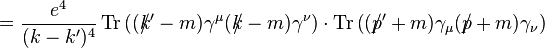






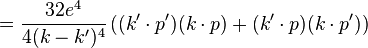




 where
where 

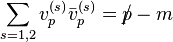
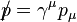 (see
(see 
 's is zero
's is zero







